2023-06-04:你的音樂播放器里有 N 首不同的歌,
在旅途中,你的旅伴想要聽 L 首歌(不一定不同,即,允許歌曲重復,
請你為她按如下規則創建一個播放列表,
每首歌至少播放一次,
一首歌只有在其他 K 首歌播放完之后才能再次播放。
返回可以滿足要求的播放列表的數量。
由于答案可能非常大,請返回它模 10^9 + 7 的結果。
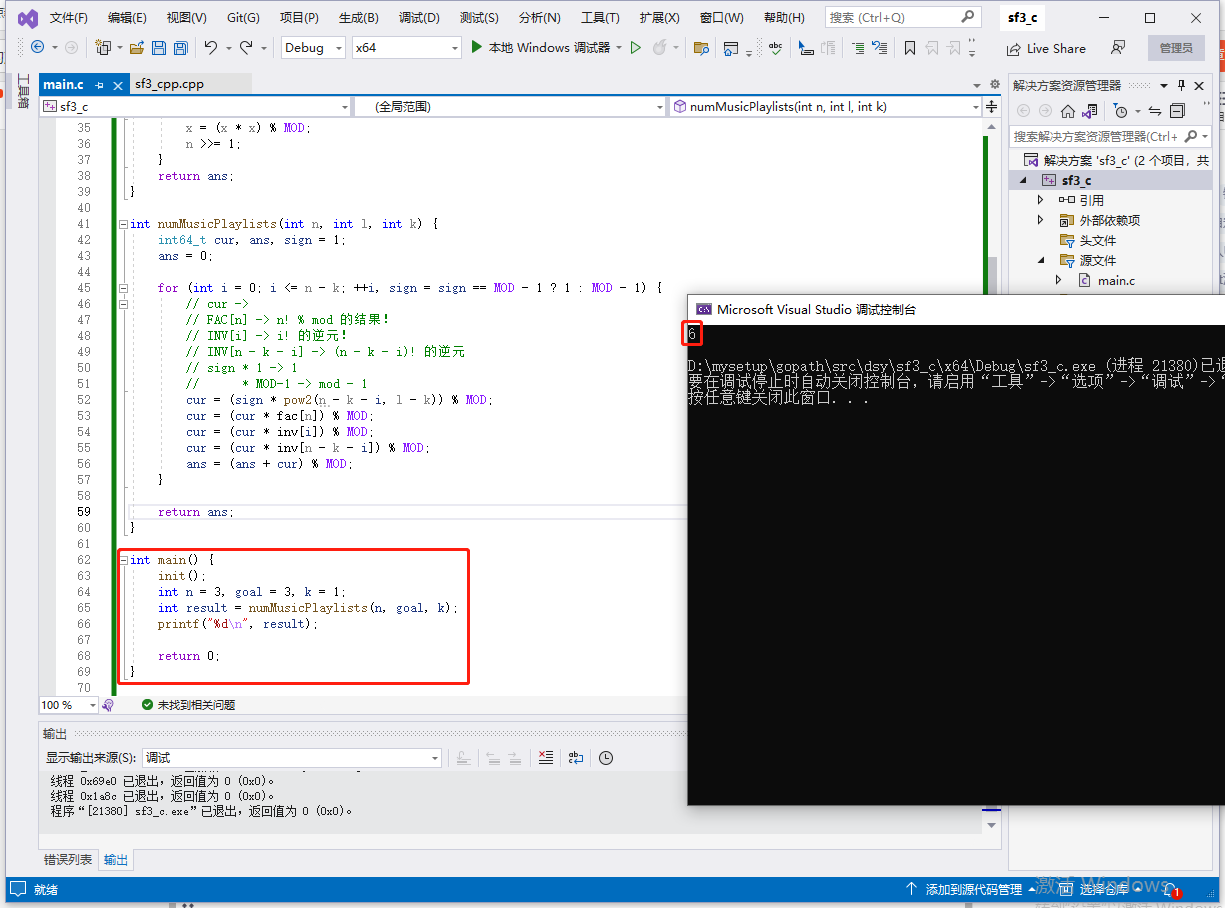
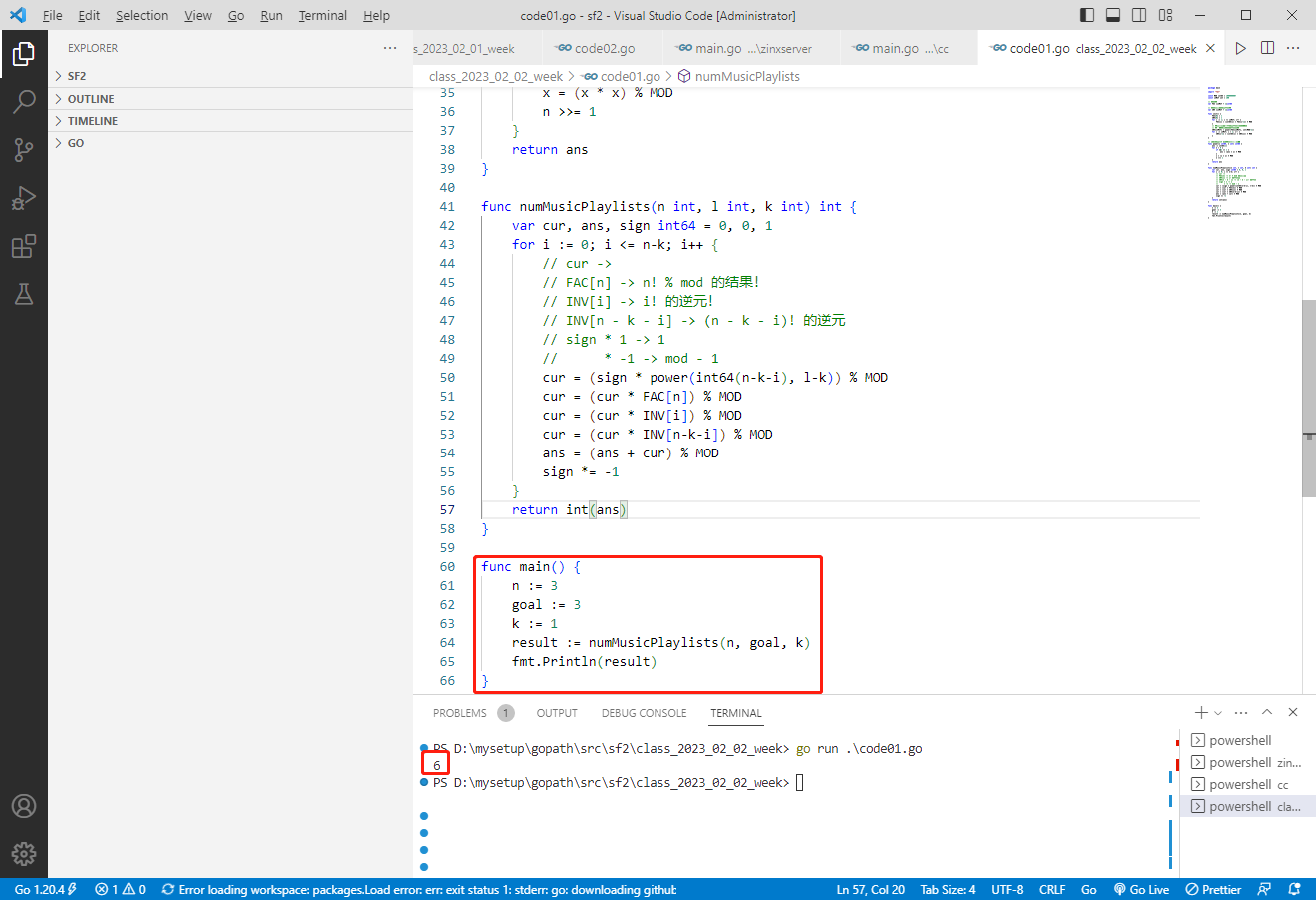
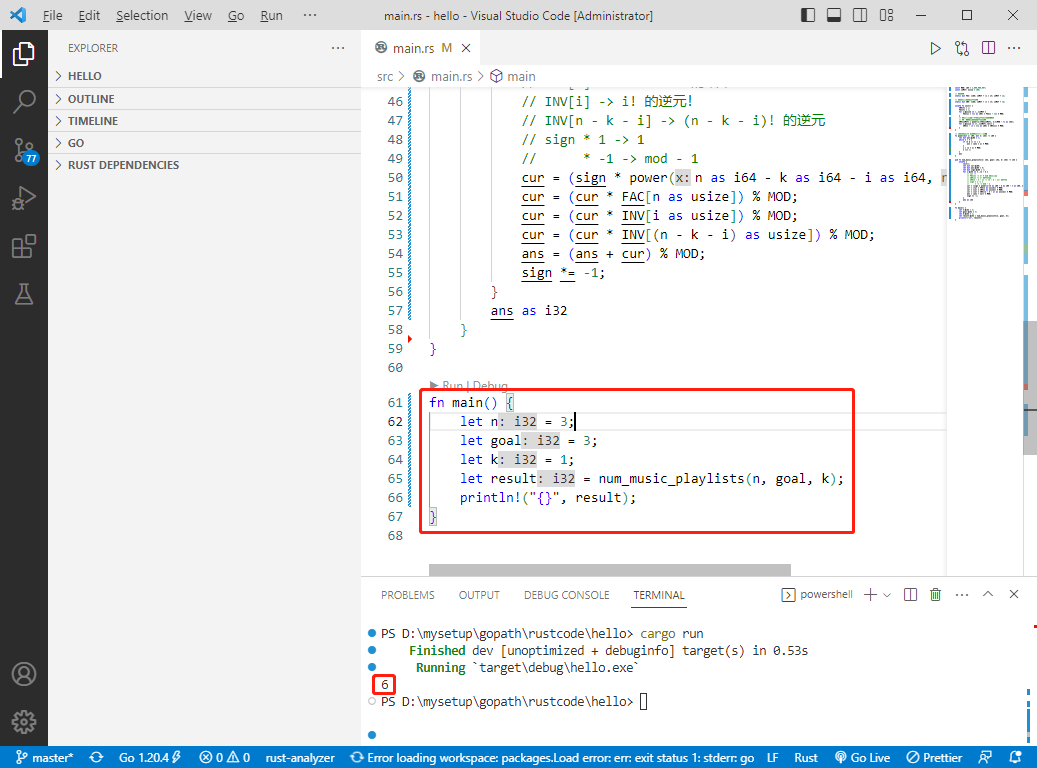
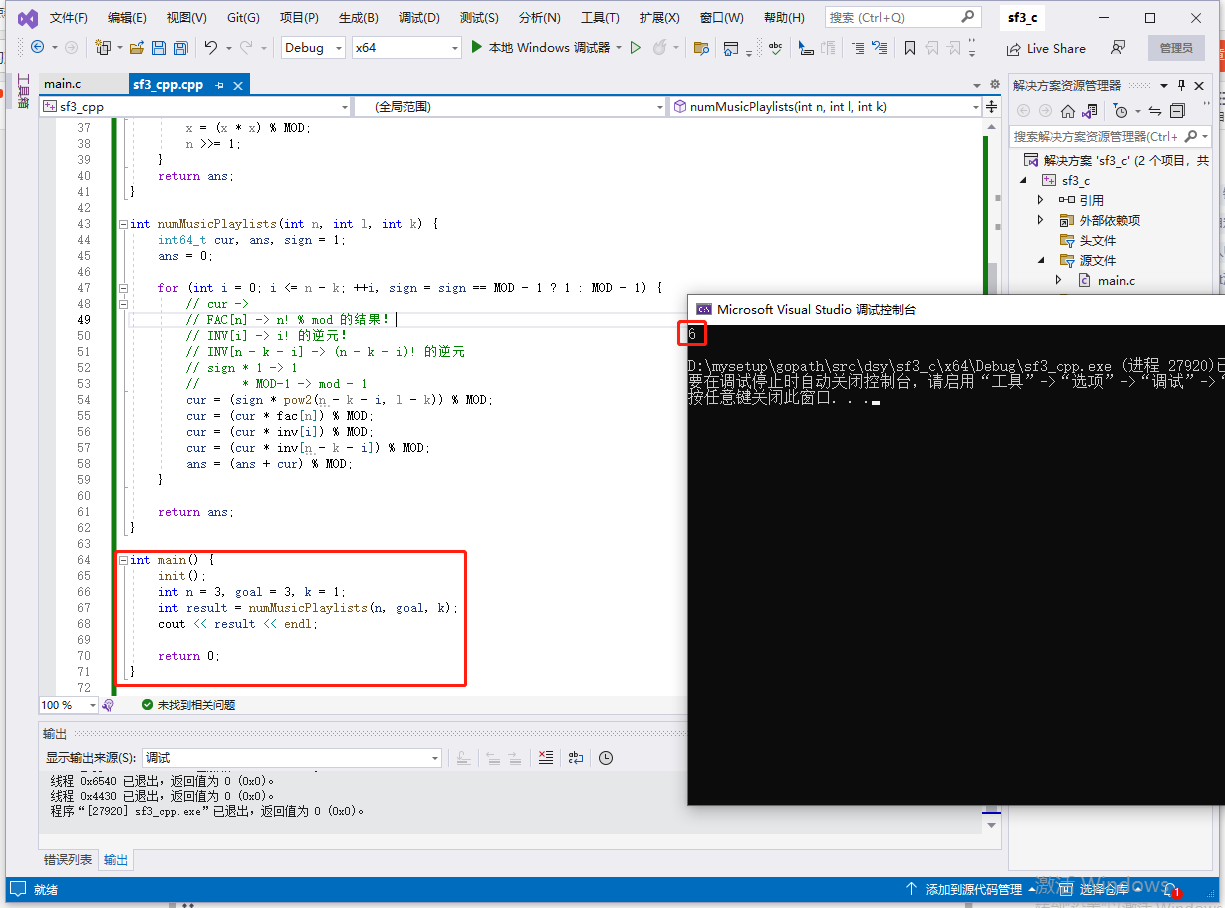
輸入:n = 3, goal = 3, k = 1。
輸出:6。
答案2023-06-04:
# 大體步驟如下:
1.定義常量MOD和LIMIT,分別表示模數和階乘表的最大值。
2.定義全局變量FAC和INV,分別表示階乘表和階乘結果的乘法逆元表。
3.編寫init函數,用于初始化FAC和INV數組。在該函數中先將FAC[0]和INV[0]賦值為1,然后使用循環計算FAC[i](i從1到LIMIT)的值,并使用費馬小定理倒推計算出INV[i](i從LIMIT到2)的值。
4.編寫power函數,用于計算x的n次方并對MOD取模后的結果。
5.編寫numMusicPlaylists函數,根據題目要求計算可以滿足要求的播放列表數量。該函數中定義三個int64類型變量:cur、ans和sign。cur用于保存當前循環中需要累加到答案中的部分,ans則是最終結果。sign初始為1,在每次循環結束時將其乘以-1來實現交替相加或相減。
6.numMusicPlaylists函數中使用一個for循環遍歷i從0到n-k。在每次循環中,首先計算cur = sign * pow(n-k-i, l-k) % MOD。其中pow函數調用了power函數來計算冪次方。
7.然后將cur乘以FAC[n]、INV[i]、INV[n-k-i]并分別對MOD取模,更新cur的值。
8.將cur加到ans中并對MOD取模,最后返回ans的int類型值。
時間復雜度:$O(n^2)$,其中n為歌曲數量。需要計算階乘表和階乘結果的乘法逆元表,時間復雜度均為O(n)。在numMusicPlaylists函數中使用了一個for循環,循環次數為n-k,每次循環中調用了power函數,時間復雜度為$O(logMOD)$,然后進行了常數次乘、除和取模運算,時間復雜度為O(1)。因此總時間復雜度為$O(n*(n-k)*logMOD)=O(n^2*logMOD)$。
空間復雜度:O(n),主要是用來存儲階乘表和階乘結果的乘法逆元表。
# go完整代碼如下:
```go
package main
import "fmt"
const MOD int64 = 1000000007
const LIMIT int = 100
// 階乘表
var FAC [LIMIT + 1]int64
// 階乘結果的乘法逆元表
var INV [LIMIT + 1]int64
func init() {
FAC[0] = 1
INV[0] = 1
for i := 1; i <= LIMIT; i++ {
FAC[i] = (int64(i) * FAC[i-1]) % MOD
}
// 費馬小定理計算乘法逆元,優化如下
// 這一塊叫:階乘的逆元倒推
INV[LIMIT] = power(FAC[LIMIT], int(MOD-2))
for i := LIMIT; i > 1; i-- {
INV[i-1] = (int64(i) * INV[i]) % MOD
}
}
// x的n次方,% mod之后,是多少?
func power(x int64, n int) int64 {
ans := int64(1)
for n > 0 {
if n&1 == 1 {
ans = (ans * x) % MOD
}
x = (x * x) % MOD
n >>= 1
}
return ans
}
func numMusicPlaylists(n int, l int, k int) int {
var cur, ans, sign int64 = 0, 0, 1
for i := 0; i <= n-k; i++ {
// cur ->
// FAC[n] -> n! % mod 的結果!
// INV[i] -> i! 的逆元!
// INV[n - k - i] -> (n - k - i)! 的逆元
// sign * 1 -> 1
// * -1 -> mod - 1
cur = (sign * power(int64(n-k-i), l-k)) % MOD
cur = (cur * FAC[n]) % MOD
cur = (cur * INV[i]) % MOD
cur = (cur * INV[n-k-i]) % MOD
ans = (ans + cur) % MOD
sign *= -1
}
return int(ans)
}
func main() {
n := 3
goal := 3
k := 1
result := numMusicPlaylists(n, goal, k)
fmt.Println(result)
}
```
# rust完整代碼如下:
```rust
const MOD: i64 = 1_000_000_007;
const LIMIT: usize = 100;
// 階乘表
static mut FAC: [i64; LIMIT + 1] = [0; LIMIT + 1];
// 階乘結果的乘法逆元表
static mut INV: [i64; LIMIT + 1] = [0; LIMIT + 1];
unsafe fn init() {
INV[0] = 1;
FAC[0] = 1;
for i in 1..=LIMIT {
FAC[i] = ((i as i64) * FAC[i - 1]) % MOD;
}
// 費馬小定理計算乘法逆元,優化如下
// 這一塊叫:階乘的逆元倒推
INV[LIMIT] = power(FAC[LIMIT], (MOD - 2) as i32);
for i in (2..=LIMIT).rev() {
INV[i - 1] = ((i as i64) * INV[i]) % MOD;
}
}
// x的n次方,% mod之后,是多少?
fn power(mut x: i64, mut n: i32) -> i64 {
let mut ans = 1;
while n > 0 {
if (n & 1) == 1 {
ans = (ans * x) % MOD;
}
x = (x * x) % MOD;
n >>= 1;
}
ans
}
pub fn num_music_playlists(n: i32, goal: i32, k: i32) -> i32 {
unsafe {
init();
let mut cur;
let mut ans = 0;
let mut sign = 1;
for i in 0..=n - k {
// cur ->
// FAC[n] -> n! % mod 的結果!
// INV[i] -> i! 的逆元!
// INV[n - k - i] -> (n - k - i)! 的逆元
// sign * 1 -> 1
// * -1 -> mod - 1
cur = (sign * power(n as i64 - k as i64 - i as i64, goal as i32 - k)) % MOD;
cur = (cur * FAC[n as usize]) % MOD;
cur = (cur * INV[i as usize]) % MOD;
cur = (cur * INV[(n - k - i) as usize]) % MOD;
ans = (ans + cur) % MOD;
sign *= -1;
}
ans as i32
}
}
fn main() {
let n = 3;
let goal = 3;
let k = 1;
let result = num_music_playlists(n, goal, k);
println!("{}", result);
}
```
# c++完整代碼如下:
```cpp
#include <iostream>
#include <vector>
using namespace std;
const int MOD = 1000000007;
const int LIMIT = 100;
// 階乘表
vector<int64_t> fac(LIMIT + 1);
// 階乘結果的乘法逆元表
vector<int64_t> inv(LIMIT + 1);
int64_t pow2(int64_t x, int n);
void init() {
fac[0] = inv[0] = 1;
for (int i = 1; i <= LIMIT; i++) {
fac[i] = ((int64_t)i * fac[i - 1]) % MOD;
}
// 費馬小定理計算乘法逆元,優化如下
// 這一塊叫:階乘的逆元倒推
inv[LIMIT] = pow2(fac[LIMIT], MOD - 2);
for (int i = LIMIT; i > 1; i--) {
inv[i - 1] = ((int64_t)i * inv[i]) % MOD;
}
}
// x的n次方,% mod之后,是多少?
int64_t pow2(int64_t x, int n) {
int64_t ans = 1;
while (n > 0) {
if (n & 1) {
ans = (ans * x) % MOD;
}
x = (x * x) % MOD;
n >>= 1;
}
return ans;
}
int numMusicPlaylists(int n, int l, int k) {
int64_t cur, ans, sign = 1;
ans = 0;
for (int i = 0; i <= n - k; ++i, sign = sign == MOD - 1 ? 1 : MOD - 1) {
// cur ->
// FAC[n] -> n! % mod 的結果!
// INV[i] -> i! 的逆元!
// INV[n - k - i] -> (n - k - i)! 的逆元
// sign * 1 -> 1
// * MOD-1 -> mod - 1
cur = (sign * pow2(n - k - i, l - k)) % MOD;
cur = (cur * fac[n]) % MOD;
cur = (cur * inv[i]) % MOD;
cur = (cur * inv[n - k - i]) % MOD;
ans = (ans + cur) % MOD;
}
return ans;
}
int main() {
init();
int n = 3, goal = 3, k = 1;
int result = numMusicPlaylists(n, goal, k);
cout << result << endl;
return 0;
}
```
# c完整代碼如下:
```c
#include <stdio.h>
#include <stdint.h>
#define MOD 1000000007
#define LIMIT 100
// 階乘表
int64_t fac[LIMIT + 1];
// 階乘結果的乘法逆元表
int64_t inv[LIMIT + 1];
int64_t pow2(int64_t x, int n);
void init() {
fac[0] = inv[0] = 1;
for (int i = 1; i <= LIMIT; i++) {
fac[i] = ((int64_t)i * fac[i - 1]) % MOD;
}
// 費馬小定理計算乘法逆元,優化如下
// 這一塊叫:階乘的逆元倒推
inv[LIMIT] = pow2(fac[LIMIT], MOD - 2);
for (int i = LIMIT; i > 1; i--) {
inv[i - 1] = ((int64_t)i * inv[i]) % MOD;
}
}
// x的n次方,% mod之后,是多少?
int64_t pow2(int64_t x, int n) {
int64_t ans = 1;
while (n > 0) {
if (n & 1) {
ans = (ans * x) % MOD;
}
x = (x * x) % MOD;
n >>= 1;
}
return ans;
}
int numMusicPlaylists(int n, int l, int k) {
int64_t cur, ans, sign = 1;
ans = 0;
for (int i = 0; i <= n - k; ++i, sign = sign == MOD - 1 ? 1 : MOD - 1) {
// cur ->
// FAC[n] -> n! % mod 的結果!
// INV[i] -> i! 的逆元!
// INV[n - k - i] -> (n - k - i)! 的逆元
// sign * 1 -> 1
// * MOD-1 -> mod - 1
cur = (sign * pow2(n - k - i, l - k)) % MOD;
cur = (cur * fac[n]) % MOD;
cur = (cur * inv[i]) % MOD;
cur = (cur * inv[n - k - i]) % MOD;
ans = (ans + cur) % MOD;
}
return ans;
}
int main() {
init();
int n = 3, goal = 3, k = 1;
int result = numMusicPlaylists(n, goal, k);
printf("%d\n", result);
return 0;
}
```